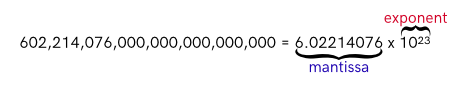In this article, we will learn several techniques for checking floating-point numbers for equality.
If we do not properly understand how floating-point values are stored internally, we might inadvertently write floating-point equality checks that do not behave as intended. Because of the ease of writing the code incorrectly, we need to be extra careful when comparing floating-point values. Throughout this article, we will examine different methods we can employ to check floating-point numbers for equality.
Before we begin, we need to look at what floating-point types are available to us and how they are stored internally. This will help us to understand the root of the problem and then we can look at a couple of different ways in which we can handle it.
Floating-Point Types
In C# we have four floating-point types available to us. These are Half, float, double, and decimal. We also have an immutable NFloat type designed for use as an exchange type at the managed/unmanaged boundary, but we will not discuss it in our article.
Half, float and double are IEEE 754 floating-point types and are 16, 32, and 64-bit values respectively. If you are using .NET 7 or 8, you will notice that each implements the IFloatingPointIeee754<T> interface.
decimal is a 128-bit floating point type (which in .NET 7 and 8 implements IFloatingPoint<T>), but is not an IEEE 754 binary floating-point. Instead, it is a limited-precision decimal type, similar to an IEEE 754 number, with the exception that the exponent is interpreted as base 10 rather than base 2 which prevents some of the unexpected rounding errors that we will see in this article. For this reason, it is the recommended type to use for financial calculations. Due to this difference, we will exclude decimal from our analysis here.
While we are not doing a deep dive on floating-point types in this article, to understand why equality checks can be problematic, we need to cover a few basics of how they are represented internally.
For a more in-depth look at floating-point types, check out our article here.
Floating-Point Number Basics
The idea of a floating-point number is encoded in the name. We have a number in which the decimal point can float. This is in contrast with a fixed-point number where the decimal point is always in a fixed location. Floating-point numbers are the computer equivalent of scientific notation.
When writing numbers in scientific notation we have a base number (mantissa) and an exponent representing a power of 10. For instance, the famous Avogadro’s number is often written as 6.02214076 x 1023:
6.02214076 is our mantissa (also known as the significand) and 23 is our exponent. We could also write this more compactly (and with less significant digits) as 6.022e23. If we knew this number and came across another number 6.022e-23, we would instantly recognize that they are not equal. While they both share the same mantissa, the exponents are anything but equal (23 != -23).
The difference between the above scientific notation and IEEE 754 floating-point numbers is found in their base. Scientific notation numbers are decimal floating-point (base 10), while IEEE 754 numbers are binary floating-point (base 2). Internally floating-point numbers are stored as a collection of bits that represent the sign of the number, the exponent, and finally the mantissa.
Let’s use a table to examine the bit layouts of the IEEE 754 floating-point types:
| Sign | Exponent | Mantissa | |
|---|---|---|---|
| Half (16 bits) | 1 | 5 | 10 |
| float (32 bits) | 1 | 8 | 23 |
| double (64 bits) | 1 | 11 | 52 |
Now with some basics on floating-point numbers fresh in our minds, let’s jump in and look at some of the problems we need to be aware of when dealing with floating-point values.
The Problem With Rounding
As we mentioned earlier, IEEE 754 numbers are stored as binary floating-point numbers. While they enable us to store a wide range of values, due to the nature of scaling, they do not always allow us to store a value exactly. Let’s look at a simple example:
Console.WriteLine(0.1 + 0.2);
What would we expect the output to be? Most likely we are expecting this code to print 0.3, but what is the actual output?
0.30000000000000004
What went wrong? Rounding. The numbers 0.1 and 0.2 cannot be stored exactly in binary floating-point and so the final sum has been impacted by these small rounding errors.
To illustrate the point, let’s look at the output of these two simple lines of code:
Console.WriteLine($"{0.1:G17}");
Console.WriteLine($"{0.2:G17}");
A quick note about the format string "G17". We use it to show all 17 possible digits of precision that are maintained internally by a double value. Now let’s look at the output:
0.10000000000000001 0.20000000000000001
Here we observe that the way we store floating point numbers internally can introduce a very small amount of error into our data. Now imagine we are performing these calculations in a loop to sum up a collection of double values. Even with the introduction of just this minuscule amount of error (1e-17) on each iteration, by the time we compute 1000 values, this accumulation of error can cause problems.
The Problem With Equality Checks
Most likely we already are starting to see why we might have problems when checking floating-point numbers for equality. The issues compound the more operations we perform. Let’s look at a simple example and then discuss what went wrong:
var calculation = 0.1 + 0.2;
var expected = 0.3;
Console.WriteLine($"{calculation == expected}");
Our naive expectation of this code is that the output would be True, but when we run it, the actual result is False. Why is that? Let’s print out the values of both calculation and expected and examine them:
Console.WriteLine($"{calculation:G17}");
Console.WriteLine($"{expected:G17}");
And the output:
0.30000000000000004 0.29999999999999999
Looking at these results, the reason our equality check failed is fairly obvious. 0.30000000000000004 is not equal to 0.29999999999999999. Though not equal, they are very, very close. They differ by only a single bit.
Let’s verify this by incrementing our variable expected and decrementing the variable calculation:
Console.WriteLine($"{calculation == double.BitIncrement(expected)}");
Console.WriteLine($"{double.BitDecrement(calculation) == expected}");
Both of these lines will print True. The double.BitIncrement() and double.BitDecrement() increment and decrement a given double by a single bit. More specifically they increment/decrement a given value to the smallest value that compares greater/less than a given value. What this also shows us is that, in the case of double values, there is no other value between 0.29999999999999999 and 0.30000000000000004 that can be represented exactly.
We can illustrate this point by printing those numbers with the format G17:
Console.WriteLine($"{0.29999999999999999:G17}");
Console.WriteLine($"{0.30000000000000000:G17}");
Console.WriteLine($"{0.30000000000000001:G17}");
Console.WriteLine($"{0.30000000000000002:G17}");
Console.WriteLine($"{0.30000000000000003:G17}");
Console.WriteLine($"{0.30000000000000004:G17}");
Console.WriteLine($"{0.30000000000000005:G17}");
Which yields the following output:
0.29999999999999999 0.29999999999999999 0.29999999999999999 0.30000000000000004 0.30000000000000004 0.30000000000000004 0.30000000000000004
It is precisely these rounding issues that lead to problems with equality checks. The more operations we perform on a floating-point number, the more error can accrue within the calculation.
Techniques for Checking Floating-Point Number Equality
There are several different techniques we can employ when checking floating-point equality. In this article, we will take a look at three of these techniques, discussing how and why they work. Understanding these techniques will aid us later when deciding which technique to employ in our code.
For each of our examples, we will use double values, as we can safely upcast to double from both float (which has an intrinsic cast to double already) and Half with no loss of precision:
const double a = 1.12345; const double b = 1.1234500000000012;
The absolute value of their difference is 1.1102230246251565E-15.
Checking Floating-Point Equality to a Specified Decimal Place
The first technique we will explore is by limiting the amount of precision in our equality check. If we know that the precision of our computation is only to 3 decimal places, then we only need to perform our check to the third decimal place. Let’s take a look at how we might accomplish this.
First, let’s create a pre-computed table of negative powers of 10 divided by 2. We are only computing up to 1e-17 as double internally maintains a maximum of 17 decimal places:
private static readonly double[] HalfNegativePowersOf10 =
{
1e0 * 0.5,
1e-1 * 0.5,
// ... omitted for brevity ...
1e-17 * 0.5
};
We will use these values in our calculation to account for rounding to the midpoint of the precision. For example, if we are computing to two decimal places of precision, using this table 0.01 will be equal to both 0.0051 and 0.015, but not 0.016 or 0.005.
And now, let’s implement our comparison method:
public static bool EqualityUsingPrecision(double a, double b, int decimalPlaces)
{
if (double.IsNaN(a) || double.IsNaN(b))
return false;
if (double.IsInfinity(a) || double.IsInfinity(b))
return a == b;
return double.Abs(a - b) < HalfNegativePowersOf10[decimalPlaces];
}
The first thing we must check is whether either of the values are NaN, that is, whether they are an actual number. NaN values are not equal to any other values, including themselves. The second thing we do is check whether either of the numbers is infinity (positive or negative). If either of them is infinity, we can simply perform a default equality check as only infinity is equal to infinity and their signs must match. Once we have handled the special cases, we simply compute the difference between the two values and then check to see if it is within the bounds of the specified precision.
Note for simplicity’s sake, we are not validating that decimalPlaces is in range, but rather allowing the framework to throw an IndexOutOfRangeException if it is an unsupported value. We can always add a check at the beginning of the function if we want to provide a more detailed error message.
Let’s see it in action:
Console.WriteLine(FloatingPointComparisons.EqualityUsingPrecision(a, b, 14)); Console.WriteLine(FloatingPointComparisons.EqualityUsingPrecision(a, b, 15));
And the output:
True False
Checking Floating-Point Equality Using a Maximum Tolerance
Another technique we can use when comparing two floating point numbers is to define an absolute tolerance or margin of error that is acceptable to declare the two numbers equal. Choosing this value is up to us based on the precision of the numbers we are dealing with. If our values have a lot of precision, we can go with something like 1e-15, but if we only have a few digits of precision, then maybe 1e-3 would be a better choice.
This time, we will make use of the Generic Math functionality available to us in .NET 7.0. This allows us to write one method that will apply to any IFloatingPointIeee754<T> type:
public static bool EqualityComparisonWithTolerance<T>(T a, T b, T tolerance)
where T : IFloatingPointIeee754<T>
{
if (T.IsNaN(a) || T.IsNaN(b))
return false;
if (T.IsInfinity(a) || T.IsInfinity(b))
return a == b;
return T.Abs(a - b) < tolerance;
}
Due to our restriction to IFloatingPointIeee754<T> types, we have access to methods such as IsNaN() and IsInfinity(). Because IFloatingPointIeee754<T> is a subset of INumberBase<T>, we also have access to the Abs() method for computing absolute value.
Notice that, just as in our previous example, first we ensure that neither of the values is NaN. Second, we check whether any of the values is infinity, and in those cases use a default equality check. Then, after handling our special cases, we simply subtract and check whether the absolute difference is within the specified tolerance.
Let’s see it in action:
Console.WriteLine(FloatingPointComparisons.EqualityUsingTolerance(a, b, 1e-14)); Console.WriteLine(FloatingPointComparisons.EqualityUsingTolerance(a, b, 1e-15));
And the output:
True False
Checking Floating-Point Equality Based on Units in Last Place
This last technique may appear a bit strange and counterintuitive at first glance, but when we think about the binary layout of floating-point values, it begins to make sense. We have already seen part of this idea in action when we called the BitIncrement() and BitDecrement() methods from double. So let’s jump right in and see how it works.
Adjacent Floating-Point Numbers Have Adjacent Integer Representations
While it may seem weird, this fact is actually due to a very careful design decision when creating the IEEE 754 standard. If we take a look at the .NET 7.0 source code, we see this behavior being used internally in the BitIncrement() function:
long bits = BitConverter.DoubleToInt64Bits(x); // ... omitted for brevity bits += ((bits < 0) ? -1 : +1); return BitConverter.Int64BitsToDouble(bits);
First, we see the conversion from double to long (internally just a simple type cast). The intervening code, omitted for brevity, handles the edge cases of infinity, NaN and -0.0. After that, there is a simple increment or decrement of the long value depending on whether the value is negative or not. Then the last step is to convert the long back to double (again, just a type cast).
So what does this mean and how does it help us deal with equality comparisons? Let’s press on and see.
Computing the Difference of the Integer Representations
Earlier we discussed the fact that due to the nature of how floating-point math works, the more calculations we do, the more small errors can accrue in our final results. These small errors are just incremental bit drifts away from what we are expecting.
Let’s use one of our earlier examples to help illustrate this point:
var calculation = 0.1 + 0.2;
var expected = 0.3;
Console.WriteLine($"{calculation == expected}");
As we saw earlier, this prints out False, contrary to what we would have naturally expected.
Now, let’s look a little deeper and see where the difference lies:
var calculationBits = *(long*)(&calculation);
var expectedBits = *(long*)(&expected);
Console.WriteLine($"{long.Abs(calculationBits - expectedBits)}");
The output of this code is 1. The value is 1 because the two floating-point numbers are adjacent. That is, there is only a single bit that separates these two floating-point values from each other. We call this difference Units in the Last Place or ULP for short. For our example, we can say that the numbers differ by 1 ULP. The smaller the number of ULPs, the closer the two numbers are to each other.
With this knowledge in hand, we can now look at how we can apply it when checking floating-point numbers for equality.
Putting It All Together
Now, let’s create our method for checking equality based on ULP:
public static bool EqualityUsingMaxUnitsInLastPlace(double a, double b, long maxUnitsInLastPlace)
{
if (maxUnitsInLastPlace < 1)
throw new ArgumentOutOfRangeException(nameof(maxUnitsInLastPlace));
if (double.IsNaN(a) || double.IsNaN(b))
return false;
if (double.IsInfinity(a) || double.IsInfinity(b) || a.IsNegative() != b.IsNegative())
return a == b;
return long.Abs(BitConverter.DoubleToInt64Bits(a) - BitConverter.DoubleToInt64Bits(b)) <= maxUnitsInLastPlace;
}
First, we need to ensure that the value for maxUnitsInLastPlace is at least 1. If it isn’t, then we need to throw an ArgumentOutOfRangeException. This is necessary as we are going to compute the absolute value of the difference, which will never be negative. Secondly, a difference of 0 means the two values are binary equal. This is not a problem, but if we want to check absolute binary equality, we can just use the default == comparison. That means any value for maxUnitsInLastPlace that is less than 1 just doesn’t make sense.
Now, the second thing we need to do is deal with some edge cases. This means, once again, we check for NaN and return false if either of the arguments are NaN.
The third if statement is slightly different than our earlier versions. We still check for infinity and perform a normal equality check in that case, but in addition to infinity, we need to ensure the signs match. That is, whether they are both positive or negative. Logically this is pretty obvious, as numbers with different signs are not equal.
This is required to handle one other special: 0.0 and -0.0. IEEE 754 floating-point numbers have two zero values, which by definition, are equal to each other. We can verify that with a simple line of code:
Console.WriteLine(0.0 == -0.0);
We need to ensure that we correctly return true when we compare 0.0 and -0.0. The method IsNegative(), which you can find in our source code, accomplishes this.
In the last line of the method we compute the ULP difference and ensure it is less than or equal to the maximum specified difference.
Let’s see it in action:
Console.WriteLine(FloatingPointComparisons.EqualityUsingMaxUnitsInLastPlace(a, b, 5)); Console.WriteLine(FloatingPointComparisons.EqualityUsingMaxUnitsInLastPlace(a, b, 4));
And the output:
True False
Benchmarks for Checking Floating-Point Equality
Let’s run a few benchmarks and see how the numbers stack up:
| Method | Mean | Error | StdDev | |-------------------------------------- |---------:|----------:|----------:| | CheckEqualityUsingTolerance | 4.554 us | 0.0104 us | 0.0081 us | | CheckEqualityUsingPrecision | 5.032 us | 0.0138 us | 0.0122 us | | CheckEqualityUsingMaxUnitsInLastPlace | 5.746 us | 0.0253 us | 0.0224 us |
From the benchmark results, we see that the method using a concrete tolerance performs the fastest, but there is not a large difference between any of the three techniques. Since they are all so close in performance, the technique we choose will depend on the data we are dealing with and what approach fits best in our situation.
Conclusion
In this article, we have seen why we need to be careful when comparing floating-point numbers. We have also looked at three different techniques for checking floating-point values for equality. From our benchmarks, we saw that there isn’t a great difference in performance between the three methods.
Ultimately, various factors including the expected range of values and their precision will affect the decision on which technique we use. If we expect our values to be fairly close to several significant digits, then we would probably check for equality within a constant tolerance. If our values may vary in their significant digits, then we probably want to use either a precision value or max ULP, that way we can adjust more easily at runtime.