In this article, we’ll look at the heap sort algorithm in C#. We’ll discuss what the algorithm is, how it works, and see some code examples that demonstrate how to implement it. Finally, we’ll discuss its time and space complexity and compare the algorithm to other sorting algorithms, such as merge sort and quick sort.
So without further ado, let’s begin!
What is Heap Sort?
Heap sort is a sorting algorithm that uses a binary heap data structure. It works by first creating a binary heap from the elements that we need to sort.
A binary heap is a complete binary tree in which each node has a value that is greater than or equal to the values of its children (if any). Once we create the binary heap, we can extract the root element and remove it from the heap.
The remaining elements can then be heapified to maintain the properties of a binary heap. We repeat this process until all elements have been extracted from the heap and are in order.
Let’s take a deep dive and learn how heap sort works.
How Does Heap Sort Algorithm Work?
The heap sort algorithm is a sorting technique that belongs to the family of comparison-based sorting algorithms. It uses a data structure called a heap, which is essentially a binary tree with some special properties. The heap sort algorithm has two phases:
1) The heapify phase: In this phase, we transform the input array into a max heap – a binary tree in which the value of each node is greater than or equal to the value of its children nodes. This can be done by starting at the last non-leaf node in the tree and working backward towards the root, ensuring that each node satisfies the max heap property.
2) The sort phase: In this phase, the max heap is repeatedly removed until only one element remains. This is done by swapping the root node with the last element in the heap, and then ensuring that the new root node satisfies the max heap property. This process is repeated until only one element remains in the heap.
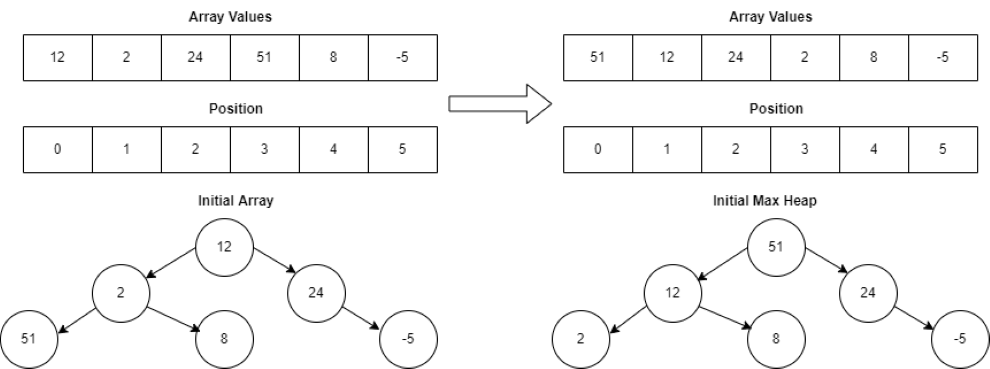
Let’s look at an example of how heap sort works. We will use the following set of numbers:
int[] array = {12, 2, 24, 51, 8, -5};
The first step is to transform the array into a max heap whereby, the largest element of the array resides at the root. Here, we see the visual representation of the array as a binary tree and its max heap representation:
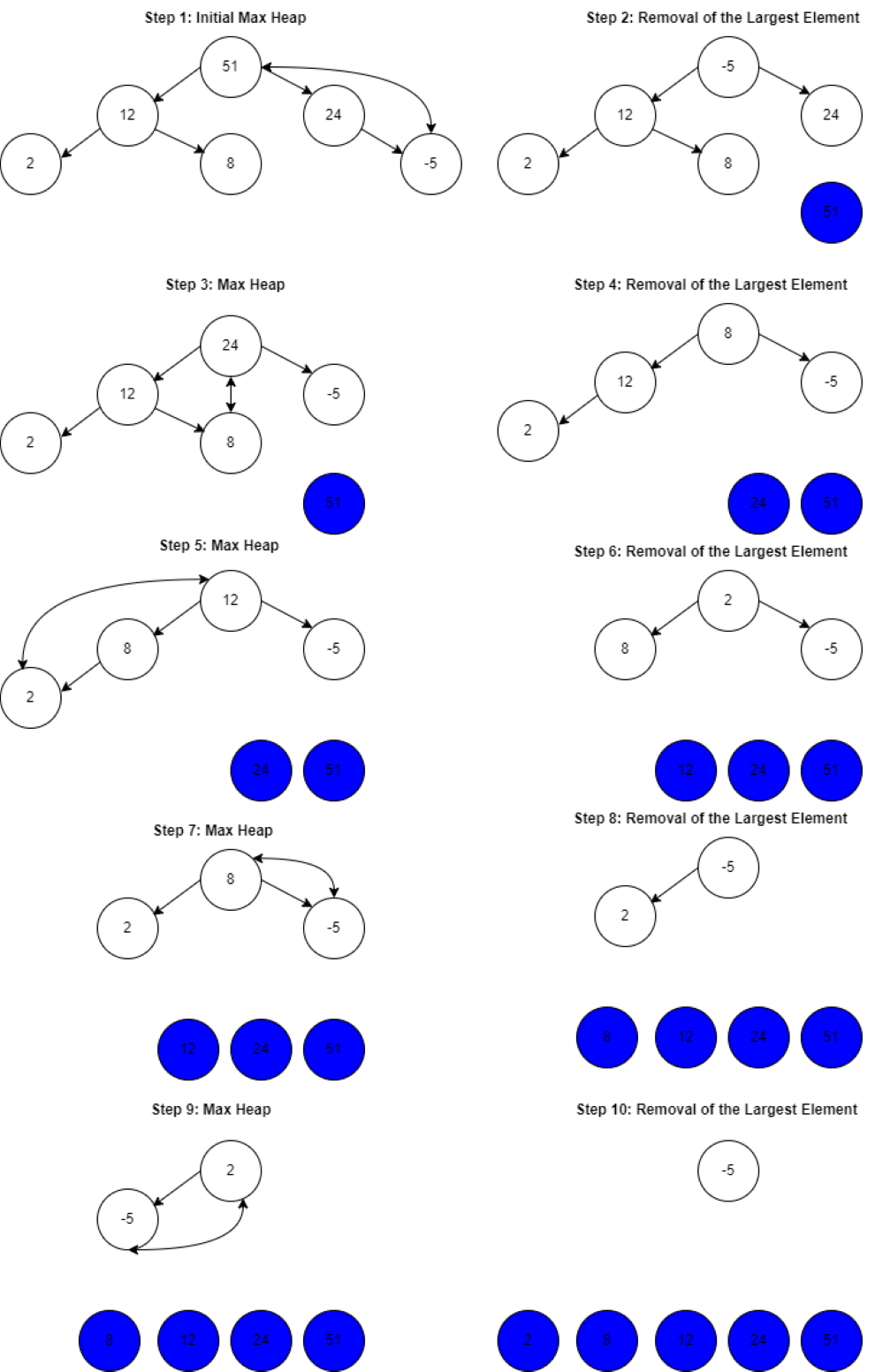
Once we build the initial max heap, we swap the last element of the heap with the current root of the element and remove the last element containing the largest element from the heap.
We apply the heapify function to convert the heap into a max heap and repeat the last step until the number of elements in the heap is one. When we reach this point, the array’s elements are in ascending order.
Let’s visualize the steps we are going to take to sort our current example:
After step 9, the sorting process is complete and the array becomes:
-5, 2, 8, 12, 24, 51
Let’s learn how to implement the heap sort algorithm in C#.
How to Implement Heap Sort in C#?
Let’s write a function SortArray() that takes an array and its size as inputs and returns a sorted list of elements:
public int[] SortArray(int[] array, int size)
{
if (size <= 1)
return array;
for (int i = size / 2 - 1; i >= 0; i--)
{
Heapify(array, size, i);
}
for (int i = size - 1; i >= 0; i--)
{
var tempVar = array[0];
array[0] = array[i];
array[i] = tempVar;
Heapify(array, i, 0);
}
return array;
}
Let’s understand how the code works.
After checking whether the array has one element or is empty, the first loop calls the Heapify() function which builds the max heap:
for (int i = size / 2 - 1; i >= 0; i--)
{
Heapify(array, size, i);
}
In the second loop, we swap the last element of the max heap with the first element, rebuild the max heap, and return the sorted array:
for (int i = size - 1; i >= 0; i--)
{
var tempVar = array[0];
array[0] = array[i];
array[i] = tempVar;
Heapify(array, i, 0);
}
return array;
Next, let’s implement the Heapify() function, which takes an array, its size, and the first element of the array as arguments:
static void Heapify(int[] array, int size, int index)
{
var largestIndex = index;
var leftChild = 2 * index + 1;
var rightChild = 2 * index + 2;
if (leftChild < size && array[leftChild] > array[largestIndex])
{
largestIndex = leftChild;
}
if (rightChild < size && array[rightChild] > array[largestIndex])
{
largestIndex = rightChild;
}
if (largestIndex != index)
{
var tempVar = array[index];
array[index] = array[largestIndex];
array[largestIndex] = tempVar;
Heapify(array, size, largestIndex);
}
}
Max Heap Implementation
Let’s understand how the Heapify() function works. First, we set the index of the maximum element to the current array index and set the left and right children elements:
var largestIndex = index; var leftChild = 2 * index + 1; var rightChild = 2 * index + 2;
Next, we check if the left child is greater than the current root element and swap their positions if the condition is true:
if (leftChild < size && array[leftChild] > array[largestIndex])
{
largestIndex = leftChild;
}
We repeat the same process and check if the right child is greater than the current root element and swap their positions if true:
if (rightChild < size && array[rightChild] > array[largestIndex])
{
largestIndex = rightChild;
}
On the other hand, if the index of the maximum element in the array is not equal to the current index, we swap the positions of array[largestIndex] and array[index] and recursively call the Heapify() function on the affected subtree until we build the max heap:
if (largestIndex != index)
{
var tempVar = array[index];
array[index] = array[largestIndex];
array[largestIndex] = tempVar;
Heapify(array, size, largestIndex);
}
Finally, we can verify that the HeapSort() method sorts a given unsorted array accurately:
var array = new int[] { 73, 57, 49, 99, 133, 20, 1 };
var expected = new int[] { 1, 20, 49, 57, 73, 99, 133 };
var sortFunction = new HeapSortMethods();
var sortedArray = sortFunction.SortArray(array, array.Length, string.Empty);
Assert.IsNotNull(sortedArray);
CollectionAssert.AreEqual(sortedArray, expected);
Space and Time Complexity of Heap Sort Algorithm
Heap sort has a space complexity of O(N) with N being the size of the array. On top of that, from our implementation, we do not require any additional space to implement the algorithm.
Best-Case Time Complexity
The heap sort algorithm encounters its best-case time complexity when it encounters identical elements. Therefore. when we have N number of elements:
- Removing every node from the heap takes constant time O(1).
- Since all elements are equal, we don’t need to keep building the max heap, hence the algorithm takes N * O(1) time or O(N).
However, since this scenario is rare, we can conclude that the best-case time complexity of the heap sort algorithm is O(N log N).
Average-Case Time Complexity
The heap sort algorithm has an average-case time complexity of O(N log N) just like its best-case time complexity. This scenario occurs when we use random array elements. The Heapify() function would have an average runtime of O(N log N) making it its average-case time complexity.
Worst-Case Time Complexity
Heap sort has a worst-case time complexity of O(N log N) just like its average-case time complexity. The algorithm is highly likely to encounter this case when all the elements are distinct.
This means we need to call the Heapify() function every time we remove an element from the heap.
Advantages of Heap Sort Algorithm
Heap sort is an in-place sorting algorithm. This means it does not require additional storage for the heap data structure when we implement it using arrays.
Besides that, the algorithm does not require any extra space to run unlike sorting algorithms such as merge sort.
Heap sort performs better than other sorting algorithms such as insertion sort and bubble sort.
Disadvantages of Heap Sort Algorithm
Heap sort is not a stable sorting algorithm. This means that if there are two elements with the same key value, their order in the sorted array is not necessarily maintained just like quicksort.
It is not as simple to implement as other algorithms such as bubble sort.
Performance Tests
Let’s test how long the algorithm takes for it to sort three arrays that have 2,000,000 elements each. To help us complete these tests, we are going to implement three methods.
First, let’s write a method to generate a set of random array elements:
public static int[] CreateRandomArray(int size, int lower, int upper)
{
var array = new int[size];
var rand = new Random();
for (int i = 0; i < size; i++)
array[i] = rand.Next(lower, upper);
return array;
}
The CreateRandomArray() the method takes three integers size, lower and upper. Using the inbuilt Random class, we generate integer values between lower and upper that we’re going to put into the array, which we are going to use to test the average-case time complexity.
Next, we are going to simulate the worst-case time complexity scenario by defining a method CreateSortedArray() that returns a sorted array (every element is going to be distinct):
public static int[] CreateSortedArray(int size)
{
var array = new int[size];
for (int i = 0; i < size; i++)
array[i] = i;
return array;
}
To simulate the best-case time complexity scenario, we are going to define a method CreateIdenticalArray() that populates the array with the same elements:
public static int[] CreateIdenticalArray(int size, int lower, int upper)
{
var array = new int[size];
var rand = new Random();
var selectedElement = rand.Next(lower, upper);
for (int i = 0; i < size; i++)
{
array[i] = selectedElement;
}
return array;
}
Here, we see that we select a random number and populate the array with that selected number.
Sample Array Objects
We are going to create an object that holds different arrays that have random and sorted values:
public IEnumerable<object[]> SampleArrays()
{
yield return new object[] { CreateSortedArray(2000000), 2000000, "Worst Case" };
yield return new object[] { CreateRandomArray(2000000, 1, 2000000), 2000000, "Average Case" };
yield return new object[] { CreateIdenticalArray(2000000, 1, 2000000), 2000000, "Best Case" };
}
Each object entry has two values: an integer array e.g. CreateRandomArray(2000000, 1, 2000000) and a string object storing the name of that array (“Average Case”). This object sorts random numbers between 1 and 2,000,000, to distribute different values within the range.
On the other hand, the last object invokes the CreateIdenticalArray() function, which returns an array that has the same value across all the array’s positions.
Sample Test Results
Let’s assess the sample best, average, and worst-case complexity performance results of the algorithm:
| Method | array | size | arrayName | Mean | Error | StdDev | |---------- |--------------- |-------- |------------- |----------:|---------:|---------:| | SortArray | Int32[2000000] | 2000000 | Average Case | 223.24 ms | 4.351 ms | 4.070 ms | | SortArray | Int32[2000000] | 2000000 | Best Case | 13.13 ms | 0.195 ms | 0.232 ms | | SortArray | Int32[2000000] | 2000000 | Worst Case | 210.33 ms | 2.406 ms | 2.250 ms |
As we can see, despite the algorithm sorting 2,000,000 elements, they have different runtimes.
The heap sort algorithm encounters its best-case time complexity scenario as the array has the same element in all positions. Additionally, we can see that heap sort’s average-case time complexity is achieved when we randomly select values within the range. On the other hand, when we have distinct elements in all positions, the heap sort algorithm encounters its worst-case time complexity.
The results are similar especially when comparing the worst (210.33 ms) and average-time (223.24ms) complexity simulations. We can conclude that the heap sort algorithm has an overall time complexity of O(N log N). Please note that these runtimes may change depending on the number of elements and the computing resources available.
Conclusion
In this article, we have learned how heap sort in C# works and its time and space complexity. In case you’d like to learn how to implement another sorting algorithm, check out some of our other sorting algorithm articles.