With the increasing progress and interest in AI and Machine Learning, keeping track of and understanding the technologies behind powerful AI and ML systems is essential. One of these technologies is Probabilistic Programming. In this article, we will learn what it is and how it can be used in C# through the Infer.NET library.
Let’s dive in and learn more about this interesting technology.
What Is Probabilistic Programming?
Probabilistic Programming aims to write more intelligent software that can reason, learn, and adapt to the available data.
In other words, we want software capable of understanding and learning from the data. This description sounds a lot like we wanted to say “AI”, doesn’t it?
The process that makes a program “AI-like” is called reasoning backward, and we will get back to it later in the article.
Usual examples of the tasks we want to be able to accomplish with our intelligent software range from simple handwriting character recognition to recommendation systems (e.g., we want to suggest a movie to a user based on his watch and search history) to more complex financial scenario modeling, healthcare prediction, etc.
Probabilistic Programming is rooted in Bayesian statistics, a branch of statistics based on the Bayesian probability theory. The basic concept of Bayesian statistics involves using probability distribution to represent uncertainty.
Machine-learning models rely on pattern recognition to categorize or predict data. We can view these patterns as molds and the process of categorization or prediction as try-fail attempts to fit the available data into these molds. Since real life often does not play by the rules, the data does not fit our molds perfectly, and our results are not as precise as they could be. Probabilistic Programming helps us soften our molds (blur the lines) to accommodate the uncertainty in real-life data, making our molds better suited to the data we have and thus more “intelligent”.
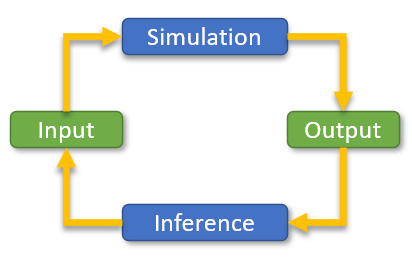
In Probabilistic Programming, information flows in both directions, from the input to the output and vice versa. The output, or the observed data, is used to infer and update input data and thus make the program better adjusted to the actual data. The following diagram illustrates this:
A Bit of History
The early development of Bayesian statistics can be traced to the end of the 18th century when Thomas Bayes, an English statistician, formulated a specific case of Bayes Theorem. Following this, Pierre-Simon Laplace, a French scholar, published several papers in which he developed the Bayesian interpretation of probability, the basis of modern Probabilistic Programming. This approach goes beyond the pure statistical understanding of probability, where probability is defined as the ratio of the number of certain events and the number of overall events that happened. Bayesian interpretation views probability as a measure of belief that a specific event will occur.
The key aspects of the Bayesian interpretation of probability are subjectivity (the rate of belief in a certain event is not the same for everyone), the incorporation of prior knowledge through subjective priors, continuous updating of beliefs with new data using Bayes’ Theorem, and the view of probability as a dynamic measure of confidence or belief rather than a fixed, long-term frequency of events.
The discovery of Markov chain Monte Carlo (MCMC) methods for sampling from a probability distribution in the 1980s provided the fundamentals for much research and applications of Bayesian methods. The discovery of MCMC helped solve computational issues associated with the Bayesian methods and opened the door for its broader adoption in many complex scenarios.
Uncertainty Example
To illustrate the real-world uncertainty, we will use a very simple example.
Let’s say we have a coin and want to determine if it is fair, but we do not have any measuring equipment.
For this, let’s design an experiment in which we toss the coin many times (e.g., a million) and record the number of heads we get. We repeat this process several times.
Let’s add some code to simulate this. For a start, we define a IsHeads() method:
private bool IsHeads { get { return Random.Shared.NextDouble() > 0.5; } }
Here, we use the Random number generator to generate a decimal number between 0 and 1. If the generated number is greater than 0.5, we consider the coin to be heads.
Next, we define a method for tossing the coin:
public int TossCoin(int numberOfRuns = 1_000_000)
{
var headsCount = 0;
for (int i = 0; i < numberOfRuns; i++)
if (IsHeads)
headsCount++;
return headsCount;
}
In this method, we “toss the coin” a specified number of times (default 1 million), returning the count of how often it came up heads.
Now, we define a IsCoinFairExperiments() method, which uses our TossCoin() method:
public int[] IsCoinFairExperiments(int numberOfExperiments = 10)
{
var headCounts = new int[numberOfExperiments];
for (int i = 0; i < numberOfExperiments; i++)
headCounts[i] = TossCoin();
return headCounts;
}
The question is whether we can determine if the coin is fair with 100% certainty from our results.
Experiment Results
We can attempt to decide the fairness based on our average number of heads. In an ideal situation, we would get heads half the time, so the average of our results should be half the number of coin tosses made. In our example, this would mean 500,000. But is this the case?
Let’s see the results for a range of experiment counts:
Experiment counts: 1 => head count average: 500020.2 Experiment counts: 10 => head count average: 500029.794 Experiment counts: 50 => head count average: 499993.576 Experiment counts: 100 => head count average: 500022.354 Experiment counts: 200 => head count average: 500007.466
Here, we see the average number is very close to the expected value, but it is not the same. So, the “coin” is slightly biased to one side.
This illustrates that a certain degree of uncertainty is present even in an example as simple as a coin toss.
Although we cannot be 100% sure, based on these results, we can be reasonably certain and infer the coin is fair because the average is much closer to 500,000 than it is to e.g., 100,000.
In other words, if a million coins are produced, we will likely pick a fair one, but there could always be cases where things don’t go according to the plan, and the result is not what we expected.
If we want to have reliable models of real-time scenarios, we need a way to incorporate this uncertainty into them. Probabilistic Programming provides us with a way to do that.
Simple Two-Coin Example
Let’s examine a slightly more complicated example with two coins. For this, we define a TossTheCoins() method in our CoinTossEngine class:
public void TossTheCoins(int numberOfRuns = 1_000_000, Func<CoinTossEngine, bool> condition = null)
{
RunCount = 0;
for (int i = 0; i < numberOfRuns; i++)
{
FirstHeads = IsHeads;
SecondHeads = IsHeads;
BothHeads = FirstHeads && SecondHeads;
if (condition == null || condition(this))
{
if (FirstHeads) FirstCoinHeadCount++;
if (SecondHeads) SecondCoinHeadCount++;
if (BothHeads) BothCoinsHeadCount++;
RunCount++;
}
}
FirstCoinPercentage = Math.Round(100.0 * FirstCoinHeadCount / RunCount, 2);
SecondCoinPercentage = Math.Round(100.0 * SecondCoinHeadCount / RunCount, 2);
BothCoinsPercentage = Math.Round(100.0 * BothCoinsHeadCount / RunCount, 2);
}
This method takes two optional parameters. First is the number of tosses, and the second defines the conditions for when to increment our counts. This will come into play in our second example.
First, let’s calculate the chances we get both heads. Since each coin has a 50% chance of getting heads and is independent of the other one, we can calculate a chance to get both heads using basic statistics. That means 0.5 x 0.5 = 0.25, which gives us a 25% chance of getting both heads.
Let’s define a test method to see this in action:
public void WhenBothHeadsTrue_ThenSuccess()
{
var coinTossEngine = new CoinTossEngine();
coinTossEngine.TossTheCoins();
Console.WriteLine($"Probability First Coin Is Heads: {coinTossEngine.FirstCoinPercentage}%");
Console.WriteLine($"Probability Second Coin Is Heads: {coinTossEngine.SecondCoinPercentage}%");
Console.WriteLine($"Probability Both Coins Are Heads: {coinTossEngine.BothCoinsPercentage}%");
Assert.AreEqual(25.0, coinTossEngine.BothCoinsPercentage, 1.0);
}
Since we deal with averages, we allow some tolerance to the expected result.
The result of this test:
Probability First Coin Is Head: 50.02% Probability Second Coin Is Head: 49.94% Probability Both Coins Are Heads: 24.95%
Here, the probability of getting both heads is approximately 25%, as expected.
Reasoning Backward Example
Now, we make it a bit more complicated. Let’s say somebody else tossed the coins and told us we didn’t get both heads. Can we calculate the chances we got heads on the first coin?
We can see the answer is not that obvious. Let’s see how we can calculate this using our code.
Since we know the final result of an experiment (both coins didn’t land as heads), we can use this to set the conditions of our experiment. So, we will disregard each toss where we did get both heads. Let’s define this in the code:
public void WhenBothHeadsNotTrue_ThenSuccess()
{
var coinTossEngine = new CoinTossEngine();
coinTossEngine.TossTheCoins(condition: m => !m.BothHeads);
Console.WriteLine($"Probability First Coin Is Heads: {coinTossEngine.FirstCoinPercentage}%");
Console.WriteLine($"Probability Second Coin Is Heads: {coinTossEngine.SecondCoinPercentage}%");
Console.WriteLine($"Probability Both Coins Are Heads: {coinTossEngine.BothCoinsPercentage}%");
Assert.AreEqual(33.0, coinTossEngine.FirstCoinPercentage, 1.0);
}
Here, we used the condition parameter to define the fact that both heads are not true:
coinTossEngine.TossTheCoins(condition: m => !m.BothHeads);
After one million of tosses, we get the results:
Probability First Coin Is Heads: 33.35% Probability Second Coin Is Heads: 33.32% Probability Both Coins Are Heads: 0%
Notice that the chance to get both heads is 0% because that is what we set as our condition. Under these conditions, we see the chance we get heads on the first coin is approximately 33%.
This is a simple example of the reasoning backward we mentioned earlier. We observed the final result and then used this information to infer the required information.
This example also illustrates the essential difference between probabilistic and classic programs. In a classical-style program, information flows only in one direction. In a probabilistic program, information can flow forward and backward.
Infer.NET
The examples we examined illustrate the basic concepts of Probabilistic Programming. But, the approach shown is far from being useful in real-world scenarios. Any real examples would require thousands of parameters and a lot of computational power to calculate the results. Therefore, this is not a practical approach.
Infer.NET is a Probabilistic Programming language (PPL, for short) developed by Microsoft Research Lab. The main goal of Infer.NET is to provide a practical way to develop machine-learning models using Probabilistic Programming.
The examples shown in this article are taken from a presentation by John Winn, one of the founders of Infer.NET.
Infer.NET has been used and proven in various applications, including social network data analysis, healthcare, internet search optimization, and computational research.
Acting as a compiler, Infer.NET converts model descriptions directly into source code and thus provides excellent performance without overhead costs.
Installation
Infer.NET packages are available through NuGet. For our project, we need to install these packages:
PM> Install-Package Microsoft.ML.Probabilistic PM> Install-Package Microsoft.ML.Probabilistic.Compiler
Example Implementations
Let’s see how to achieve the same tasks we saw in our examples using Infer.NET. First, let’s define a CoinTossInferNetEngine class:
public class CoinTossInferNetEngine
{
private readonly InferenceEngine inferenceEngine = new();
private static Variable<bool> IsHeads => Variable.Bernoulli(0.5);
public Variable<bool> FirstHeads { get; private set; }
public Variable<bool> SecondHeads { get; private set; }
public Variable<bool> BothHeads { get; private set; }
public double FirstCoinPercentage { get; private set; }
public double SecondCoinPercentage { get; private set; }
public double BothCoinsPercentage { get; private set; }
public void TossTheCoins(Action<CoinTossInferNetEngine> condition = null)
{
FirstHeads = IsHeads;
SecondHeads = IsHeads;
BothHeads = FirstHeads & SecondHeads;
condition?.Invoke(this);
FirstCoinPercentage = Math.Round(100.0 * inferenceEngine.Infer(FirstHeads).GetProbTrue(), 2);
SecondCoinPercentage = Math.Round(100.0 * inferenceEngine.Infer(SecondHeads).GetProbTrue(), 2);
BothCoinsPercentage = Math.Round(100.0 * inferenceEngine.Infer(BothHeads).GetProbTrue(), 2);
}
}
The first thing we notice is the types of data. Infer.NET works with data distributions instead of concrete values. So, instead of bool, we use Variable<bool>. Likewise, our IsHead method is defined as:
private static Variable<bool> IsHeads => Variable.Bernoulli(0.5);
To get the results, we define an InferenceEngine class instance. This is the mathematical engine that can determine the distribution of a random variable.
In the highlighted lines, we see its usage. First, we get the distribution of the required variable:
inferenceEngine.Infer<Bernoulli>(FirstHeads)
Then we use GetProbTrue() method to obtain the probability of it being true.
So, to implement the first example, we define a test method:
public void WhenBothHeadsTrue_ThenSuccess()
{
var coinTossInferNetEngine = new CoinTossInferNetEngine();
coinTossInferNetEngine.TossTheCoins();
Console.WriteLine($"Probability First Coin Is Heads: {coinTossInferNetEngine.FirstCoinPercentage}%");
Console.WriteLine($"Probability Second Coin Is Heads: {coinTossInferNetEngine.SecondCoinPercentage}%");
Console.WriteLine($"Probability Both Coins Are Heads: {coinTossInferNetEngine.BothCoinsPercentage}%");
Assert.AreEqual(coinTossInferNetEngine.BothCoinsPercentage, 25.0, 1e-3);
}
This, in turn, produces the results:
Probability First Coin Is Heads: 50% Probability Second Coin Is Heads: 50% Probability Both Coins Are Heads: 25%
In the second example, we implement reasoning backward using the ObservedValue property of the BothHeads variable:
public void WhenBothHeadsNotTrue_ThenSuccess()
{
var coinTossInferNetEngine = new CoinTossInferNetEngine();
coinTossInferNetEngine.TossTheCoins(condition: m => m.BothHeads.ObservedValue = false);
Console.WriteLine($"Probability First Coin Is Heads: {coinTossInferNetEngine.FirstCoinPercentage}%");
Console.WriteLine($"Probability Second Coin Is Heads: {coinTossInferNetEngine.SecondCoinPercentage}%");
Console.WriteLine($"Probability Both Coins Are Heads: {coinTossInferNetEngine.BothCoinsPercentage}%");
Assert.AreEqual(coinTossInferNetEngine.FirstCoinPercentage, 33.33, 1e-3);
}
In our previous example without Infer.NET, we had to set the fact that the variable BothHeads is not true as a condition of acceptance for each coin toss we did. Infer.NET enables us to set the final result and propagates that information back to inputs. It then calculates the data distributions of the FirstHeads and SecondHeads variables required for our observation to be correct. We can almost say that Infer.NET enables us to travel back in time.
As expected, the results are:
Probability First Coin Is Heads: 33.33% Probability Second Coin Is Heads: 33.33% Probability Both Coins Are Heads: 0%
We noticed there is no need to validate these test results with a large tolerance (a small tolerance is still needed due to issues with comparing floating-point equality). Infer.NET will go further than the naive statistic approach and produce expected numbers using data distributions.
Probabilistic Programming Benefits
Traditional programming approaches have difficulties in dealing with uncertainty. Probabilistic Programming lifts the curtain on the unknown and deals with uncertainty as an integral factor. Some of the benefits of machine-learning models built on Probabilistic Programming:
-
Adaptability and Continuous Learning – The ability to dynamically adjust and learn from new data over time.
- Enhanced Reasoning Capabilities – The ability to draw nuanced and informed conclusions from available data.
-
Dynamic Understanding of Uncertainty – Probabilistic Programming facilitates a nuanced understanding and representation of uncertainty within machine learning models, leading to more realistic and reliable predictions.
-
Informed Decision-Making – The software developed using Probabilistic Programming excels at making informed decisions based on its comprehension of the underlying data, contributing to more effective and context-aware outcomes.
-
Versatility Across Applications – The utility of Probabilistic Programming extends across diverse domains, including financial situation modeling and healthcare prediction models, showcasing its adaptability to complex and critical tasks.
-
Natural Handling of Uncertainty – The inherent Bayesian approach in Probabilistic Programming allows for the natural and principled handling of uncertainty, making it well-suited for tasks where the quantification and management of uncertainty are essential.
Probabilistic Programming Limitations
There are also certain limitations of Probabilistic Programming:
-
Domain Knowledge Requirement – Building effective probabilistic models often requires a good understanding of the domain. Selecting appropriate priors, specifying realistic likelihood functions, and interpreting results all benefit from domain expertise.
- Learning Curve – Probabilistic Programming frameworks can have a steep learning curve, especially for individuals new to Bayesian statistics or probabilistic modeling. Mastery of these tools often requires a solid understanding of both the underlying probabilistic concepts and the programming language.
-
Not Always Necessary – Probabilistic Programming might be overkill for certain machine learning tasks that do not inherently involve uncertainty or where simpler models suffice. In such cases, the overhead of using a Probabilistic Programming framework may outweigh the benefits.
-
Lack of Standardization – There is a lack of standardization across Probabilistic Programming languages, and the field is still evolving. This can make it challenging to port models between different frameworks or to find comprehensive documentation and support for certain languages.
-
Performance Trade-offs – Achieving both model expressiveness and computational efficiency can be challenging. There is often a trade-off between model complexity and the ability to perform efficient inference.
Conclusion
In this article, we aimed to demystify the concepts of probabilistic programming and provide a basic understanding of Infer.NET. Although introduced some 20 years ago, Infer.NET provides an interesting approach to solving modern ML and AI challenges. While this exploration was introductory, future articles will delve deeper into more complex examples and applications of Infer.NET.